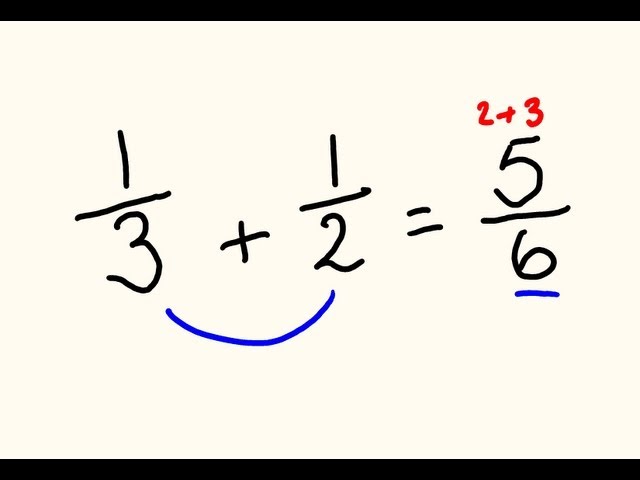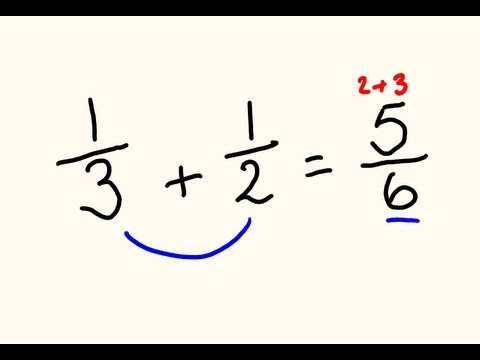How to Do Fractions: Effective Ways to Master Fractions in 2025

Mastering fractions is essential for students of all ages, whether they are just starting out or are delving into more advanced topics. **Fractions for beginners** can sometimes be overwhelming, but with the right strategies and resources, anyone can learn how to do fractions effectively. This article provides practical methods to help users, from children to adults, improve their understanding and application of fractions by 2025. We’ll go through the basics of fraction concepts, operations involving fractions, and creative learning tools that simplify the fraction learning process.

Understanding Fraction Basics

Before diving into more complex concepts, it’s crucial to grasp the fraction basics. A fraction consists of two numbers: the **numerator** (the top part) and the **denominator** (the bottom part). Together, they represent a part of a whole. Understanding this fundamental concept of improper fractions, mixed numbers, and equivalent fractions sets the stage for further learning. For instance, 1/2 is a fraction that represents one part of a whole divided into two equal parts. Recognizing the different types of fractions, such as proper and improper fractions, is vital in various mathematical contexts.

Types of Fractions

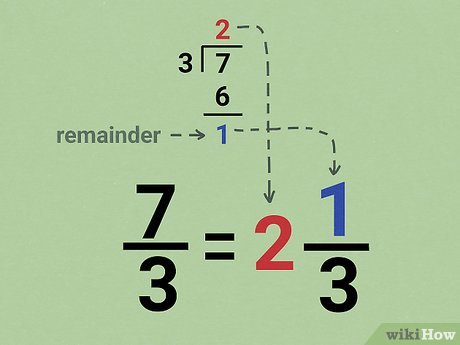
There are several types of fractions, including proper fractions, improper fractions, and mixed numbers. Proper fractions have a numerator smaller than the denominator (e.g., 3/4), while improper fractions have a numerator that is larger than or equal to their denominator (e.g., 5/4). Mixed numbers combine whole numbers and fractions (e.g., 1 ½). Recognizing and being able to convert between these types of fractions enhances one’s fraction skills significantly and helps in future calculations.

Equivalent Fractions

Equivalent fractions are different fractions that represent the same value. For example, 1/2 is equivalent to 2/4 or 3/6. Learning how to generate equivalent fractions involves multiplying or dividing both the numerator and denominator by the same number. This concept is crucial as it often appears in fraction word problems and practical applications of fractions. Understanding and applying equivalent fractions allows learners to manipulate fractions more easily when they tackle addition and subtraction of fractions.

Visualizing Fractions

Using visual aids is a powerful method to enhance understanding of fractions. Models such as pie charts, bar graphs, and number lines all help in visualizing fractions. **Visualizing fractions** makes it easier to comprehend how fractions work in reality—particularly when working with **fraction games** or **learning fractions worksheets**. These tools engage learners more actively and allow them to see fraction relationships, which ultimately deepens their understanding of the subject.

Operations with Fractions

Once students grasp the basics of fractions, they need to learn how to perform operations such as addition, subtraction, multiplication, and division of fractions. This knowledge is foundational in advancing their mathematical learning, as these operations are frequently used in everyday scenarios and specialized fields.

Addition of Fractions

When adding fractions, you must have common denominators, which can be achieved by finding the least common multiple (LCM) of the denominators. For example, to add 1/4 and 1/6, first, convert both fractions so they have a common denominator of 12. The result would be 3/12 + 2/12 = 5/12. Understanding this concept is crucial for solving complex fraction exercises and tackling real-life problems, such as measuring ingredients in recipes.

Subtraction of Fractions

The subtraction of fractions follows the same principles as addition. You need a common denominator to subtract fractions effectively. For example, when subtracting 2/3 – 1/6, convert the fractions to have a common denominator of 6, resulting in 4/6 – 1/6 = 3/6 or simplified to 1/2. Practice through **fraction worksheets** can help solidify these concepts and improve speed in calculations.

Multiplication and Division of Fractions

Multiplying fractions is direct: simply multiply the numerators together and the denominators together. For instance, 1/2 * 1/3 = 1/6. Conversely, dividing fractions involves multiplying by the reciprocal. So, to divide 1/2 by 1/3, you would calculate 1/2 * 3/1 = 3/2. Learning these operations will prepare students for higher-level mathematics as they move forward.

Engaging with Fraction Challenges

Applying languages, visuals, and creative problem-solving is essential for mastering fractions. Here’s how you can foster an engaging learning environment.

Fraction Games

Incorporating **fraction games** into learning can make mastering fractions enjoyable and practical. Online platforms and educational apps offer interactive games that challenge students to solve fraction problems while engaging in fun activities. By integrating games, learners can build their fraction skills without the pressure of traditional testing.

Real-world Applications of Fractions

Relating fractions to real-life scenarios, such as cooking, budgeting, or measuring distances, enhances learning. For instance, in fractions in cooking, understanding how to halve a recipe or convert measurements from cups to tablespoons builds practical skills. When learners grasp the connection between **fractions in real life** and their mathematical counterparts, they increasingly see the value of mastering fractions.

Using Digital Tools for Learning Fractions

Technology plays an important role in education today. There are numerous educational resources, apps, and tutorials available online that provide interactive fraction lessons. These digital tools can cater to different learning styles, be it through visual aids, **fraction manipulative tools**, or educational games. Embracing technology can significantly enhance one’s learning experience and understanding of fraction relationships.

Key Takeaways

• Understanding and mastering the *basics of fractions* is the foundation for future mathematical success.
• Learning the operations of addition, subtraction, multiplication, and division is crucial for problem-solving.
• Practicing with *fraction games* and visual models can make the learning process more engaging and effective.
• Connecting fractions to real-world applications promotes a deeper appreciation and understanding of fractions.

FAQ

1. What are the different types of fractions?

The different types of fractions include proper fractions, improper fractions, and mixed numbers. Proper fractions have a numerator that is less than the denominator, while improper fractions have a numerator equal to or greater than the denominator. Mixed numbers combine whole numbers and fractions. Recognizing these types is essential in understanding fraction concepts.

2. How can I simplify a fraction?

To simplify a fraction, divide both the numerator and denominator by their greatest common divisor (GCD). For example, if you have the fraction 8/12, the GCD is 4. So, dividing both by 4 gives you the simplified fraction of 2/3. Learning this process enhances your fraction skills and enables you to solve fraction problems more efficiently.

3. Why are equivalent fractions important?

Equivalent fractions are important because they allow us to understand the relationship between different fractions that represent the same value. This concept is essential in addition and subtraction when finding a common denominator, making it easier to perform calculations in various real-life and academic contexts.

4. What are some effective strategies for teaching fractions?

Effective strategies for teaching fractions include using visual aids and models, interactive fraction games, and real-world applications of fractions. Implementing these methods engages learners and helps them relate fractions to their everyday experiences, enhancing their learning outcomes.

5. How can I practice fractions at home?

You can practice fractions at home by utilizing online resources and interactive tutorials that provide worksheets and exercises. Fraction games and visual tools can also make the practice more enjoyable and effective. Consider integrating fractions into daily cooking or baking activities as a practical application to enhance understanding.

6. Where can I find additional resources for learning fractions?

There are numerous websites and educational platforms that offer free worksheets, tutorials, and interactive games focused on mastering fractions. Websites like Khan Academy and educational YouTube channels are excellent places to start, and they provide a variety of learning materials suitable for different age groups and skill levels.

7. How do fractions relate to other math concepts?

Fractions relate to various mathematical concepts, including decimals, percentages, ratios, and algebra. Understanding how to manipulate and interpret fractions effectively can significantly enhance your capabilities in more advanced mathematics and real-world applications, such as statistics and financial literacy.